Maximum Likelihood Estimation in Finance: All You Need to Know

What is Maximum Likelihood Estimation?

Maximum Likelihood Estimation (MLE) is a statistical method for estimating parameters in probability distributions. We select settings that maximise the a priori chance of the desired outcome occurring.

A Short Example

You have three hats with uniformly distributed random numbers. One hat’s numbers have a mean of zero and a standard deviation of 0.1. This is Hat A. Another hat’s numbers have a mean of 0 and a standard deviation of 1. This is Hat B. The final hat numbers have a mean of zero and a standard deviation of 10. This is Hat C. You’re not sure which hat is which.

Picking a number from one hat yields -2.6. Which hat do you believe it originated from? MLE can assist you in answering this question.

A Deep Dive into Maximum Likelihood Estimation

Identifying model parameters is a key aspect of statistical modelling. Maximum Likelihood Estimation is a prominent method for doing this.

A simple example can quickly demonstrate the process. You’re attending a maths conference. You go by train to the event location. You can take a taxi from the train station to the conference venue.
The taxi number is 20922. How many taxis are present in the city?

This is a parameter estimation problem. Taking a specific cab is a probability occurrence. Estimating the number of cabs in the city based on that incident requires assumptions and statistical methodology.

For this problem the obvious assumptions to make are:

1. Taxi numbers are strictly positive integers
2. Numbering starts at one
3. No number is repeated
4. No number is skipped

We will analyse the likelihood of using cab number 20,922 when there are N taxis in the city. Getting into a specific taxi is as straightforward as it gets,

Which N maximizes the probability of getting into taxi number 20,922? The answer is

N = 20,992

This example demonstrates the notion of MLE, which involves selecting parameters that increase the likelihood of the desired outcome occurring.

Another Example for Maximum Likelihood Estimation

The hat example above is more applicable to quantitative finance issues. You have three hats with uniformly distributed random numbers. One hat’s numbers have a mean of zero and a standard deviation of 0.1. This is Hat A. Another hat’s numbers have a mean of 0 and a standard deviation of 1.
This is Hat B. The final hat numbers have a mean of zero and a standard deviation of 10. This is Hat C.

You pick a number out of one hat, it is −2.6. Which hat do you think it came from?

The chance of selecting the number -2.6 from hat A (with a mean of zero and a standard deviation of 0.1) is,

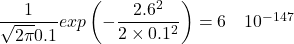
Very, very unlikely!

The word ‘probability’ is in inverted commas to emphasize the fact that this is the value of the probability density function, not the actual probability. The probability of picking exactly −2.6 is, of course, zero.

The chance of selecting the number -2.6 from hat B (with a mean of zero and a standard deviation of one) is,

and from hat C (having a mean of zero and a standard deviation of 10)

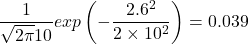
Hat C is the most likely option for selecting the value -2.6. We select a second number from the same hat, which is 0.37. This appears to have originated in hat B. We get the table of probability shown below.

HAT	-2.6	0.37	Joint
A		0.004
B	0.014	0.0372	0.005
C	0.039	0.040	0.002

The second column shows the likelihood of drawing -2.6 from each hat, the third column shows the probability of drawing 0.37 from each hat, and the last column shows the joint probability of drawing both numbers from each hat.

Based on the information from both drawings, the most likely hat is B. Now let’s make this into precisely a quant finance problem.

Find the Volatality

You have one hat containing normally distributed random numbers with a mean of zero and an unknown standard deviation (). You draw N numbers () from this hat. Estimate .

What is the ‘probability’ of drawing from a Normal distribution with mean zero and standard deviation ?

What is the ‘probability’ of drawing all the numbers from independent Normal distributions with mean zero and standard deviation ()?

Now, select the σ that maximises this quantity. This is easy. First, logarithm the expression, then differentiate with respect to σ, then put the result equal to zero.

A multiplicative factor has been ignored here.

Therefore our best guess for σ is given by,

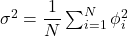
You should recognize this as a measure of the variance.

Related Readings

• Modern Portfolio Theory in Finance
• Arbitrage in Quantitative Finance: All You Need To Know
• Modelling Approaches in Quantitative Finance: All You Need To Know
• Put-Call Parity: All You Need To Know