What is Market Price of Risk?
The market price of risk refers to the desired return over the risk-free rate as compensation for taking on risk.

A Short Example
Historically a stock has increased by an average of 20% per annum when the risk-free rate of interest was 5%. Throughout this time, there was 30% volatility. Consequently, this stock returns an extra 0.5 percent on average above the risk-free rate for every unit of risk. This is the market price of risk.
A Deep Dive into Market Price of Risk
According to conventional economic theory, only an individual who anticipates outpacing the return on holding a risk-free asset would make an investment in a risky asset. Usually, volatility or the standard deviation of returns is used to calculate risk.
A stock’s market price of risk can be calculated by dividing the standard deviation of returns by the ratio of expected return over the risk-free interest rate. Remarkably, leverage has no effect on this amount. The market price of risk remains constant if you borrow money at the risk-free rate to invest in a risky asset, as both the expected return and the risk rise. This ratio is also the Sharpe ratio when appropriately annualised.
What is the market price of risk for an option on a stock, given that the stock has a given market price of risk? This is a natural question to ask. In the well-known Black-Scholes universe, where volatility is predictable and continuous and cost-free hedging is possible, the option’s market price of risk is equal to the equity’s underlying price. This has to do with the idea of a complete market, wherein options are superfluous as stock and cash can do the same job.
We frequently attempt to model quantities in derivatives theory as stochastic, or random. Risk follows randomness, and risk raises the question of how to value risk that is, what kind of return can we reasonably hope to obtain by taking a risk? Is the amount you are modelling traded directly in the market? is by far the most significant factor that determines the role of this market price of risk.
Market Price of Risk and Hedging in Option Pricing
The Black-Scholes option pricing model does not include the market price of risk if the quantity is traded directly, with stocks being the most prominent example. This is due to the fact that you can dynamically buy and sell the underlying asset in an option position to reduce risk. The foundation of risk-neutral valuation is this.
By hedging, one can remove their exposure to both the market price of risk and the direction in which the asset is moving. If you examine the Black–Scholes equation, you will see this.
There, the growth rate and risk price are absent, and the only metric derived from the stock random walk is volatility.
In contrast, the option-pricing model will make explicit reference to the market price of risk if the modelled amount is not traded directly. This is true because associated risk cannot be hedged away.
Furthermore, since the risk cannot be hedged, you must determine how much additional return is required to offset the risk. In fact, whenever you cannot properly hedge, the market price of risk will usually show up in standard option-pricing models. Thus, be prepared for it to show up in the following scenarios:
- when a quantity that is not traded is represented by a stochastic model. Examples include risk of default, interest rates (this is a subtle one, the spot rate is not traded), and stochastic volatility.
- when hedging is not possible. Jump models, default models, and transaction costs are a few examples.
The equation regulating the pricing of derivatives is typically of diffusion form when modelling stochastically a quantity that is not traded, with the market price of risk appearing in the “drift” term with respect to the non-traded quantity. This is a general example to help illustrate the point.
Calibration vs. Reality: The Stochastic Market Price of Risk
Assume that the value of a quantity of a material known as phlogiston determines the price of an option. Phlogiston is not traded; however, either its value influences the underlying asset’s dynamics or the option’s payment is contingent on it. We represent phlogiston’s value as
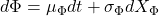
Phlogiston risk has a market price of ![]()
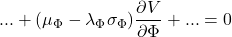
All the other terms that are often seen in an equation of the Black–Scholes type are represented by the dots. Note that the market price of phlogiston risk has been factored into the predicted change in phlogiston value, ![]()
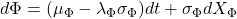
and not the real one.
If you were to look at a times series of the value of any observable financial variable, you might theoretically estimate its true drift and volatility. However, how can the market price of risk be calculated? Only option prices provide information on the market price of risk. At this juncture, practice and sophisticated theory begin to diverge. The market price of risk seems like a cool method of determining how much more value is needed to accommodate risk.
Conclusion
Sadly, there is no calmness in the way the markets respond to danger. The relationship between the market price of interest rate risk and the slope of the yield curve, for instance, is very straightforward. However, data from this implies that the market price of risk is stochastic in and of itself, and that it ought to be modelled stochastically as well.
Keep in mind that you frequently accurately calibrate the market price of risk when you tune a model to the prices of available options. However, that is usually only a moment in time captured in a snapshot. Calibration will not work if the market price of risk is random and reflects people’s fluctuating sentiments from fear to greed and back again. This is because you are assuming something that is highly mobile.
Certain models do not include the market price of risk since they usually utilise some kind of utility theory technique to determine an individual’s pricing for an instrument instead of the price set by the market.
Related Readings
- Modern Portfolio Theory in Finance
- Arbitrage in Quantitative Finance: All You Need To Know
- Modelling Approaches in Quantitative Finance: All You Need To Know
- Put-Call Parity: All You Need To Know