What is Jensen Inequality?
Jensen Inequality states that if f(.) is a convex function and x is a random variable, then
![Rendered by QuickLaTeX.com E[f(x)] \geq f\ [E(x)]](https://thewhisperingvoid.com/wp-content/ql-cache/quicklatex.com-eb36218aaf09f2db1fd2ee1058bcc39e_l3.png)
This explains why non-linear instruments and options have inherent value.

A Short Example
When you roll a die and square the number of spots, you will win the specified amount of money. In this exercise, f(x) represents ![]()
E[f(x)] = 1 + 2 + 9 + 16 + 25 + 36 = 91 divided by 6, resulting in 15 1/6. E[x] = 3 1/2, hence f(E[x]) = 12 1/4.
A Deep Dive into Jensen Inequality
A function f (·) is convex on an interval if for every x and y in that interval
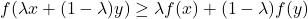
For every ![]()
(x, f (x)) and (y, f (y)) is not lower than the curve. (Concave is the reverse of convex, therefore -f is convex.)
Jensen’s inequality and convexity help explain how unpredictability in stock prices affects the value of options, which are often convex.
Assuming a random stock price S, we can calculate the value of an option with payment P(S). We may calculate the expected stock price at expiration ![]()
![]()
![]()
![Rendered by QuickLaTeX.com E[P(S_T)] \geq P(E[S_T])](https://thewhisperingvoid.com/wp-content/ql-cache/quicklatex.com-f5fa6ce429b6d729542afe035711babc_l3.png)
Using a Taylor series approximation around mean of S, we can estimate the difference between the left and right sides. Write
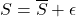
where ![]()
![Rendered by QuickLaTeX.com E[f(S)] = E[f(\overline {S} + \epsilon)] = E[f(\overline{S})+\epsilon {f}'(\overline{S}) + \dfrac{1}{2}\epsilon ^{2}{f}''(\overline{S})+ ...]](https://thewhisperingvoid.com/wp-content/ql-cache/quicklatex.com-3a1720db7f566c3b2e4f10bbf8040a5e_l3.png)
![Rendered by QuickLaTeX.com \approx f(\overline{S}) + \dfrac{1}{2}{f}''(\overline{S})E[\epsilon ^{2}]](https://thewhisperingvoid.com/wp-content/ql-cache/quicklatex.com-8aa52f16598bf6a5b44a76ddd517ef7f_l3.png)
![Rendered by QuickLaTeX.com = f (E[S]) + \dfrac{1}{2} {f}'' (E[S])E[\epsilon ^{2}]](https://thewhisperingvoid.com/wp-content/ql-cache/quicklatex.com-28487854cb8c6a523989cc8b92a8203e_l3.png)
Therefore the left-hand side is greater than the right by approximately
![Rendered by QuickLaTeX.com \dfrac{1}{2} {f}'' (E[S])E[\epsilon ^{2}]](https://thewhisperingvoid.com/wp-content/ql-cache/quicklatex.com-441010ec121cceb3ffaeeba074bd0508_l3.png)
Conclusion
This shows the importance of two concepts
![Rendered by QuickLaTeX.com {f}'' (E[S])](https://thewhisperingvoid.com/wp-content/ql-cache/quicklatex.com-5b2cf5b560fef3a333ea24e25ea4d13a_l3.png)
![Rendered by QuickLaTeX.com E[\epsilon ^{2}]](https://thewhisperingvoid.com/wp-content/ql-cache/quicklatex.com-12b9f3ea4e0c3adc33091ab0acf11194_l3.png)
When a contract contains convexity in a random variable or parameter, pricing should account for it. Identifying the level of convexity and unpredictability is necessary for accurate results.
Related Readings
- Modern Portfolio Theory in Finance
- Arbitrage in Quantitative Finance: All You Need To Know
- Modelling Approaches in Quantitative Finance: All You Need To Know
- Put-Call Parity: All You Need To Know
great