Grisanov Theorem in Finance: All You Need to Know

What is Grisanov Theorem?

Girsanov theorem explains how to shift measurement from the real world to the risk-neutral universe. We can transition from one Brownian motion to another by using drift.

A Short Example

The classical example is to start with

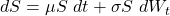
W represents Brownian motion under one measure (real-world measure) and can be converted to

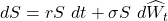
under a different, the risk-neutral, measure.

A Deep Dive into Grisanov Theorem

First, let me express the theorem. Assume is a Brownian motion with measure and sample space . If is a previsible process that meets the requirement, Then there exists an equivalent measure on such that

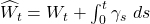
is a Brownian motion.

To better understand this theorem, we should clarify some technical words.

Sample Space

All possible future states or outcomes.

(Probability) Measure

In simple terms, the measure indicates the likelihood of each result in the sample space.

Previsible Process

A previsible process relies solely on previous history.

Equivalent

Two measures are equivalent if they have the same sample space and set of ‘possibilities.’ Note the usage of possibilities instead of probabilities. Both measures must agree on what outcomes are feasible, even if their probabilities disagree.

Another approach to write the above is in differential form.

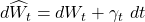
The reverse of Girsanov’s theorem states that any analogous measure can be represented by a drift change. According to the Black-Scholes model, there is only one risk-neutral measure. If this is not the case, there could be several arbitrage-free prices.

The Girsanov theorem may not be applicable to all financial problems. This is common in the field of stock derivatives. Black-Scholes is straightforward and does not require knowledge of Girsanov. Beyond the basics, Black-Scholes becomes increasingly useful. Consider deriving partial differential equations for options with stochastic volatility. Stock prices follow real-world processes ,

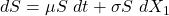
and,

and are Brownian motions with a correlation of .

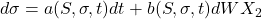
Girsanov provides the controlling equation in three steps:

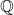
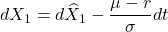
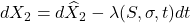
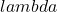
• Based on Girsanov’s pricing measure and the fact that S is traded, it follows that, and where is the market price of volatility risk
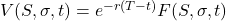
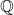
• To calculate the discounted option price, use Ito’s formula: . Expand under and use the dS and dV equations from the Girsanov transformation.
• Since the option is exchanged, the coefficient of the dt term in its Ito expansion must be 0, resulting in the relevant equation.

Girsanov’s concept of change of measure is particularly relevant in the fixed-income market, where practitioners must manage multiple measures with varying maturity levels. This is why the BGM model and similar ones are so popular.

Related Readings

• Modern Portfolio Theory in Finance
• Arbitrage in Quantitative Finance: All You Need To Know
• Modelling Approaches in Quantitative Finance: All You Need To Know
• Put-Call Parity: All You Need To Know