Greek Terminology in Finance: All You Need to Know

What is Greek Terminology in Finance?

The Greek Terminology or simply the ‘greeks’ refer to the price sensitivity of derivatives to various underlyings, factors, and parameters. Differentiating option values with regard to variables and/or parameters can be determined analytically or numerically, depending on the available closed-form formula.

A Short Example into Greek Terminology

Delta, , is the sensitivity of option prices to stock prices. Gamma, , is the second derivative of the option price with respect to the underlying stock; it represents the delta’s sensitivity to the stock price. These two samples are named greek since they belong to the Greek alphabet. Some sensitivities, such as Vega = are not part of the Greek alphabet, but they are still referred to as ‘greek’.

A Deep Dive into Greek Terminology

Delta

The delta, of an option or portfolio of options indicates its sensitivity to the underlying asset. It refers to the rate at which an asset’s value changes.

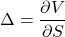
Speculators predict the direction of a quantity, such as asset prices, and use a technique to profit from it. If someone owns options, their exposure to the underlying is roughly equivalent to owning the underlying’s delta.

Those who do not speculate on the direction of the underlying will hedge by purchasing or selling the underlying or another option, resulting in a portfolio delta of zero. By doing so, they eliminate market risk.

To maintain a delta-neutral position, the number of assets held must be adjusted regularly based on stock price and time. Rehedging, often known as rebalancing the portfolio, is a form of dynamic hedging.

To short a stock for hedging, it may be necessary to borrow the stock first.
(You then sell what you have borrowed, buying it back later.) Borrowing money might be pricey, as you may need to pay a repo rate, which is similar to an interest rate.

Gamma

The gamma, , of an option or portfolio represents the position’s second derivative in relation to the underlying asset.

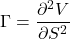
Gamma refers to the delta’s sensitivity to its surroundings and determines how frequently a position needs to be rehedged to remain delta-neutral. If there are fees connected with purchasing or selling stocks, such as the bid-offer spread, the stronger the gamma, the higher the friction produced by dynamic hedging.

To minimise expenses and limit model error, it’s natural to avoid frequent portfolio rebalancing. A gamma-neutral technique can reduce the need for hedging by reducing the sensitivity of the hedge ratio to underlying market volatility. This involves purchasing or selling multiple ‘options’, not simply the underlying.

Theta

Theta, or , represents the rate of change in the option price over time. The Black-Scholes equation relates theta to the option value, delta, and gamma.

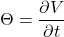
Speed

The speed of an option is the rate of change of the gamma with regard to the stock price.

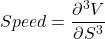
Traders use the gamma to estimate how much they will have to rehedge by if the stock moves. The stock moves by $1 therefore the delta changes by whatever the gamma is.
But that’s merely an approximation. The delta may change by more or less than this, especially if the stock moves by a bigger amount, or the option is close to the strike and expiration. Hence the usage of speed in a higher-order Taylor series expansion

Vega

The vega, often known as zeta or kappa, is a significant yet complex variable. This refers to the sensitivity of option prices to volatility.

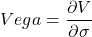
This Greek derivation differs from others in that it refers to a ‘parameter’ rather than a ‘variable’. This could be essential. It’s permissible to assess the sensitivity of a variable that varies. Measuring sensitivity to a parameter, such as volatility, might be problematic as it may be believed to be constant. That would be internally inconsistent.

As with gamma hedging, one can vega hedge to reduce sensitivity to the volatility. This is a huge step towards eliminating some model risk, since it minimises dependence on a variable that is not known very correctly.

There is a downside to the measurement of vega. It is only really meaningful for options having single-signed gamma everywhere. For example it makes sense to measure vega for calls and puts but not binary calls and binary puts. The reason for this is that call and put values (and options with single-signed gamma) have values that are monotonic in the volatility: increase the volatility in a call and its value increases everywhere.
Contracts with a gamma that changes sign may have a vega calculated at zero because when we increase the volatility the price may climb somewhere and fall some- where else. Such a contract is particularly vulnerable to volatility risk yet that risk is not assessed by the vega.

Rho

, is the sensitivity of the option value to the interest rate used in the Black-Scholes formula:

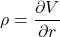
Interest rates are typically expressed as a time-dependent rate, denoted by r(t). Rho represents the sensitivity to rate changes over time, assuming a parallel shift.

Rho can also be affected by dividend yield or foreign interest rates in a foreign exchange option.

Charm

The charm is delta’s sensitivity to time.

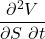
This is important for predicting how your hedge position will evolve over time, such as until the next time you plan to hedge. This can be essential when the expiration date approaches.

Colour

The colour represents the pace at which gamma changes over time.

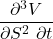
Vanna

The Vanna represents delta’s sensitivity to volatility.

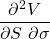
This is used to examine the sensitivity of hedging ratios to volatility. Small gamma values might be deceiving.

Vomma or Volga

The Vomma or Volga is the second derivative of option value based on volatility.

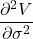
Jensen’s Inequality indicates that if volatility is stochastic, the Vomma/Volga measure convexity owing to random volatility, providing guidance on how much to add or deduct from an option value.

Shadow Greeks in Greek Terminology

The above greeks are defined in terms of partial derivatives with regard to the underlying, time, volatility, etc. while holding the other variables/parameters constant. This is the definition of partial derivatives. However, in practice, the variables/parameters may shift simultaneously. For example, a decline in stock price may be accompanied by an increase in volatility.
Sensitivity can be measured by tracking both the underlying and volatility movements simultaneously. This is known as a shadow Greek and is similar to the idea of total derivative in fluid mechanics, where one may track the motion of a fluid particle.

.

Related Readings

• Modern Portfolio Theory in Finance
• Arbitrage in Quantitative Finance: All You Need To Know
• Modelling Approaches in Quantitative Finance: All You Need To Know
• Put-Call Parity: All You Need To Know