CrashMetrics In Finance: The Ultimate Tutorial You Should Know

What is CrashMetrics?

CrashMetrics is a stress-testing methodology that evaluates portfolio performance during significant market swings. Similar to Capital Asset Pricing Model (CAPM), it only applies to significant changes in individual stocks and indices. This applies to equity portfolios and derivatives.

A Short Example to understand CrashMetrics

Your portfolio includes numerous individual stocks and derivatives of various types. This strategy takes advantage of your market knowledge and volatility to profit. What if the market falls by 5%? How will this impact your profit and loss? What if the collapse is 10%, 20%…?

A Deep Dive into CrashMetrics

CrashMetrics is a basic risk-management tool for analysing the impact of a market-wide shift. It is useful for investigating situations where diversification is not effective.

If your portfolio consists of a single underlying equity and its derivatives, the change in value during a crash, , can be expressed as , where F(·) is the ‘formula’ for the portfolio, meaning option-pricing formulae for all of the derivatives and equity in the portfolio, and is the change in the underlying.

In CrashMetrics the risk in this portfolio is measured as the worst case over some range of equity moves:

worst-case loss =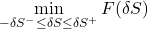 

This value represents the potential downside during a significant market movement.

Taming the Downside: Optimize Your Portfolio with Platinum Hedging

To mitigate this disadvantage, consider strategically incorporating derivatives into your portfolio. This is called Platinum Hedging. If you want to employ out-of-the-money puts to mitigate the worst-case scenario, you can optimise by selecting .

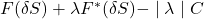
The formula for calculating the change in value of a hedging contract is F(·), with C representing the contract’s cost and λ representing the contract quantity to be determined. In actuality, there may be multiple hedging contracts, such as an out-of-the-money put, which should be combined and optimised.

CrashMetrics leverages stocks’ high correlation during extreme markets to cope with several underlyings. During a crash, we can compare the return on the ith stock to that of a representative index, .

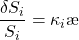     where 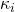 is crash coefficient

For example, if the for stock XYZ is 1.2 it means that when the index falls by 10% XYZ will fall by 12%. The crash coefficient therefore allows a portfolio with many underlyings to be interpreted during a crash as a portfolio on a single underlying, the index. We therefore consider the worst case of

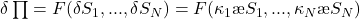
as our measure of downside risk.

Again Platinum Hedging can be applied when we have many underlyings. We must consider the worst case of

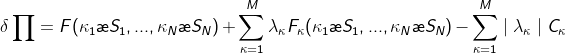
where F is the original portfolio and the are the available hedging contracts.

A Good Risk Tool

• Simple and fast to implement
• Used to optimize portfolio insurance against market crashes

Robust

• It does not use unstable parameters such as volatilities or correlations
• It does not rely on probabilities, instead considers worst cases

Use Cases

• Analyzing derivatives portfolios under the threat of a crash
• Optimizing portfolio insurance
• Reporting risk
• Providing trading limits to avoid intolerable performance during a crash

Related Readings

• Value At Risk in Finance: All You Need To Know
• Arbitrage in Quantitative Finance: All You Need To Know
• Modelling Approaches in Quantitative Finance: All You Need To Know
• Central Limit Theorem In Finance: Power Your Portfolio Now
• Capital Asset Pricing Model