Cointegration in Finance: All You Need To Know

What is Cointegration?

Cointegration of two time series refers to a linear combination with a constant mean and standard deviation. The two series remain consistent. Cointegration is an effective tool for examining relationships in multivariate time series and modelling long-run and short-run dynamics in a financial system.

A Short Example

If you have two stocks, and , and remains stationary, the combination will never deviate from the mean. If the ‘spread’ becomes too high, there are statistical reasons to believe it will soon decrease, perhaps leading to arbitrage profit. This can be the foundation for pairs trading.

A Deep Dive into Cointegration

Financial correlations are notoriously fragile. Nonetheless, correlations are commonly exploited in multivariate financial situations. Cointegration is an alternative statistical measure to correlation. Although this may be a more reliable measure of the relationship between two financial quantities, there is currently limited derivatives theory based on it.

Two equities may be perfectly connected at short timescales yet diverge in the long run, with one growing and the other degrading. Two stocks may have a positive, negative, or fluctuating correlation while being separated by a specific distance. Short-term correlation may be important for delta hedging, while unhedged portfolios with long-term holdings may not.

To determine if two stocks remain close together, we need to define stationarity. A time series is stationary if it has a fixed mean, standard deviation, and autocorrelation function. Stocks tend to expand and are not static. Stationary series remain relatively close to their mean value.

Testing for the stationarity of a time series involves a linear regression to find the coefficients a, b and c in

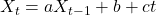
If it is discovered that |a| > 1, the series is unstable. If −1 < a < 1, the series is stationary. If a=1, the series is non-stationary. Our statistical value for a may only be considered accurate with a certain level of confidence. To determine whether a series is stationary or non-stationary, we use the Dickey-Fuller statistic to quantify the degree of confidence in our results. However, the concept of cointegration becomes more complex from here.

How can this help in finance? While individual stock prices may not be stationary, a linear combination, such as a portfolio, can still be stationary. Can we find with so that

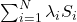
is stationary? If we can, then we say that the stocks are cointegrated.

Consider a portfolio of 15 equities that is correlated with the S&P500. We can utilise the fifteen stocks to track the index. This tracking portfolio’s error will have a constant mean and standard deviation, ensuring it does not deviate from the average.

This method is more efficient than tracking all 500 stocks, which would result in zero tracking errors.

Instead of tracking the index, we can use to select a portfolio with a 20% return. Analysing the cointegration features of linked equities, such as Nike and Reebok, can reveal potential links. This would be pairs trading. MPT and CAPM share concepts like means and standard deviations. Cointegration requires fewer properties for each time series compared to other methods. Most significantly, volatility and correlation are not expressly stated.

Cointegration also includes Granger causality, which occurs when one variable leads and another lags behind. This helps explain why there is a dynamic link between various financial metrics.

Related Readings

• Modern Portfolio Theory in Finance
• Arbitrage in Quantitative Finance: All You Need To Know
• Modelling Approaches in Quantitative Finance: All You Need To Know
• Put-Call Parity: All You Need To Know