What is Brownian Motion?
Brownian Motion is a stochastic process with stationary independent, normally distributed increments and continuous sample pathways. This is the most commonly used stochastic building component for random walks in finance.

A Short Example
Brownian motion can be observed in several environments, including pollen in water, smoke in a room, and pollution in rivers. This model also applies to stock prices.
A Deep Dive into Brownian Motion
Brownian motion (BM) was called after the Scottish botanist who first documented the random movement of pollen grains suspended in water. Bachelier and Einstein formalised the mathematics behind this approach in the context of option pricing. BM involves heat conduction and diffusion.
BM is a continuous, stationary stochastic process with normally distributed increments. If ![]()
t, then for every t, ![]()
![]()
![]()
![]()
The important properties of BM are as follows.
- Finiteness: Scaling the variance with each time step is important for BM to remain finite.
- Continuity: The pathways are continuous, with no discontinuities. However, the path is fractal and cannot be differentiated anywhere.
- Markov: The conditional distribution of
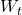

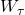
- Martingale: Given knowledge up to

Wtis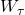
- Quadratic Variation: if we divide up the time
0totin a partition withn + 1partition points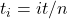
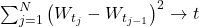
- Normality: Over finite time increments
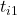
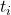
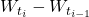
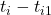
Pro’s of Brownian Motion
BM is a basic yet powerful tool for modelling random processes, particularly in finance. Its simplicity enables calculations and analysis that are not achievable with other procedures. For example, in option pricing, simple closed-form equations are used to calculate the prices of vanilla options. BM can be used to create random walks with unique properties.
Mean-reverting random walks are commonly used to model interest rates. Higher-dimensional variants of BM can depict multi-factor random walks, such as stock prices with stochastic volatility.
Con’s of Brownian Motion
BM produces unnaturally shallow tail distributions, which is one of its drawbacks. Asset returns typically have broader tails than the normal distribution of BM. Evidence suggests that the distribution of returns may have an infinite second instant. BM motion is the most commonly used model to depict random walks in finance, despite other theories incorporating fat tails.
Related Readings
- Modern Portfolio Theory in Finance
- Arbitrage in Quantitative Finance: All You Need To Know
- Modelling Approaches in Quantitative Finance: All You Need To Know
- Put-Call Parity: All You Need To Know