What is a Coherent Risk Measure: All You Need To Know

Introduction to Coherent Risk Measure

A risk measure is called a coherent risk measure if it meets simple mathematical requirements. Some prominent metrics lack sub-additivity, which means that combining two hazardous portfolios does not enhance the measure of risk.

A Simple Example of Coherent Risk Measure

Artzner et al. (1997) provided a straightforward example of classical VaR that contradicts this principle and highlights the issue of incoherent measurements. Portfolio X only includes an out-of-the-money put with a one-day expiration. Portfolio Y only includes an out-of-the-money call with a one-day expiry. Assume each choice has a 4% chance of becoming profitable. At 95% confidence, the typical one-day VaR for each option is zero. Combining the two portfolios results in a 92% likelihood of not losing anything, less two lots of 4%. At the 95% confidence level, there will be significant VaR. Putting the two portfolios together has in this example increased the risk. “A merger does not create extra risk” (Artzner et al., 1997).

A Deep Dive

Traditional VaR is often criticised for failing to meet key commonsense criteria. Artzner et al. (1997) established sensible criteria for a risk measure, , where X represents a set of outcomes. They are as follows.

1. Sub-Additivity: . Adding two portfolios together does not increase the total risk beyond that of adding the two hazards separately. Indeed, cancellation effects or economies of scale may help to mitigate the danger.
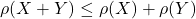
2. Monotonicity: If in all scenarios, then . If one portfolio outperforms another in all circumstances, it will have lower risk.
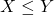
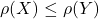
3. Positive Homogenity: For all , . If you double your portfolio, you’ll also double your risk.
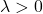
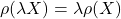
4. Translation Invariance: For any constant c,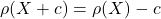 . Consider adding cash to your portfolio to reduce risk.

Coherent risk measures are those that meet all of these criteria. The classic, simple VaR measure is not coherent since it does not meet the sub-additivity criteria. A risk measure must have sub-additivity, as adding uncorrelated new trades would not provide any risk benefit. For portfolios X and Y, the benefit can be defined as:

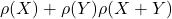
Sub-additivity says that this can only be non negative.

The lack of sub-additivity is a risk measure that can be used for regulatory arbitrage. To preserve regulatory capital, banks can construct subsidiary entities in a reverse form, as seen above.

A coherent measure of risk, with sub-additivity, allows for a cautious assessment of total risk by adding the hazards of individual portfolios together.

Coherent Measures

Coherent measurements Standard deviation is straightforward and coherent. This solution falls short as it does not address the most devastating tail events. Another cohesive measure is Expected Shortfall. This is derived as the average of all P&Ls in the tail percentile of interest. Instead of quoting the 5% percentile (conventional VaR), calculate the average of all P&Ls in the 5% tail.

Attribution

Once a risk measure is calculated, it’s common to assign it to smaller units.
For instance, a desk may analyse risk and determine each trader’s responsibility. In a derivatives portfolio, it may be beneficial to divide risk into contributions from each Greek. Consider the risk associated with market direction vs volatility exposure.

Related Readings

• Put-Call Parity: All You Need To Know
• Modelling Approaches in Quantitative Finance: All You Need To Know
• Central Limit Theorem In Finance: Power Your Portfolio Now