What are Low Discrepancy Numbers?
Low discrepancy sequences cover a space without clustering or gaps. Adding another number to the sequence prevents clustering and gaps. They offer the appearance of unpredictability, yet are predictable. They are used to numerically estimate integrals in high dimensions. Faure, Halton, Hammersley, Niederreiter, and Sobol are responsible for the most well-known sequences.

A Short Example
You have the option to pay off up to 20 exchange rates on a defined date. You understand all the volatility and correlations. How can you determine the contract’s value? Assuming lognormal random walks for exchange rates, this problem can be solved as a 20-dimensional integral. To assess high-dimensional integrals numerically, low-discrepancy sequences are an efficient method.
A Deep Dive into Low Discrepancy Numbers
Financial issues can often be reframed as integrations across multiple dimensions. The value of a European option on lognormal random variables can be expressed as the present value of the risk-neutral expected reward. The expected payout is calculated by integrating the payoff function with the probability density function for the underlying(s) at expiry. If there are n underlyings, there is usually an n-dimensional integral to calculate.
If the number of dimensions is modest, there exist efficient algorithms to execute the calculation. In one dimension, divide the region of integration into regular intervals and employ the trapezium rule. By evaluating the integrand at multiple locations, the approach becomes more accurate as the number of function evaluations rises.
In higher dimensions, evaluating functions at equally spaced points becomes computationally inefficient.
If the domain of integration is a unit hypercube (which can be turned into one), the result of the integral equals the average function over that domain.

The ![]()
N function evaluations are conducted, the approach converges in ![]()
Taming the Error: Koksma-Hlawka Inequality and Low-Discrepancy Sequences
To avoid the gapping/clustering problem, we should employ a number sequence. This is where low-discrepancy sequences come in.
Low-discrepancy numbers use the Koksma-Hlawka inequality to limit the error in averaging arbitrary collections of sample points (![]()
f(x) has bounded variation V(f), then

![]()
The key takeaway from this result is that the bound is made up of two terms: one specific to the function (its variation), which is independent of the sampling points, and one specific to the set of sampling points, which is independent of the function being sampled. Once a good set of points with low disagreement is identified, it can be applied to all integrands with bounded variation.
The typical low-discrepancy sequences listed above have
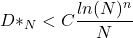
where C represents a constant. The quasi Monte Carlo numerical quadrature method converges faster than random Monte Carlo.
Low-discrepancy sequences have the advantage of avoiding repeating points when collapsed to a lower dimension, such as the horizontal axis in a two-dimensional graphic. The approach accurately distributes points over lower dimensions, even if one variable has a substantial dependence on others.
Implementing low-discrepancy sequences can still be challenging. Some practitioners choose to use off-the-shelf software to generate random integers.
Related Readings
- Modern Portfolio Theory in Finance
- Arbitrage in Quantitative Finance: All You Need To Know
- Modelling Approaches in Quantitative Finance: All You Need To Know
- Put-Call Parity: All You Need To Know
good