Most Useful Performance Measures in Finance: All You Need to Know

What are Performance Measures?

Performance measures quantify the outcome of a trading strategy. In most cases, they are risk adjusted. The Sharpe ratio is the most popular.

A Short Example of Performance Measures

One stock’s annual growth rate is 10%, whereas another’s is 30%. Would you like to invest in the second option? Is it significant that the first had 5% volatility while the second had 20%?

A Deep Dive into Performance Measures

Performance measurements assess an investment strategy’s success. When a hedge fund or trader is asked about their prior performance, the first question is typically “What was your return?”. Later, consider asking ”What was your worst month?” These are simple performance measures. Sensible measures consider the risk involved, since a high return with low risk is preferable than a high return with high risk.

Sharpe Ratio

The Sharpe ratio is a key risk-adjusted performance metric. It is calculated as:

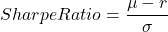
where represents the strategy’s return over a certain period, r is the risk-free rate, and is the standard deviation of returns. The Sharpe ratio will be expressed in annualised terms. A high Sharpe ratio indicates good strategy.

If returns are regularly distributed, the Sharpe ratio indicates the likelihood of earning more than the risk-free rate. In Modern Portfolio Theory’s expected return versus risk diagram, the Sharpe ratio represents the slope of the line connecting each investment to the risk-free investment. To obtain the Market Portfolio, select the portfolio with the highest Sharpe ratio. The Central Limit Theorem states that when analysing several investments, the mean and standard deviation are the most important factors. As long as the CLT is valid, the Sharpe ratio makes sense.

Critics argue that the Sharpe ratio gives equal weight to both upside and downside risk, while standard deviation takes both into account in its calculation. This may be significant if the returns are highly skewed.

Modigliani-Modigliani Measure

The Modigliani-Modigliani or M2 measure is a simple linear transformation of the Sharpe ratio:

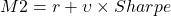
where represents the standard deviation of the relevant benchmark’s returns. This represents the expected return from a portfolio if it were de-leveraged to match the volatility of the benchmark.

Sortino Ratio

The Sortino ratio is similar to the Sharpe ratio, but employs the square root of semi-variance as the denominator to assess risk. Semi-variance is assessed similarly to variance, but replaces all positive data points with zero or a target value.

This measure absolutely overlooks ‘risk’ on the upside. For normally distributed returns, the semi-variance is statistically noisier than the variance due to the use of fewer data points in the calculation.

Treynor Ratio

The Treynor or Reward-to-variability Ratio is a Sharpe-like measure that considers systematic risk (measured by the portfolio’s beta) rather than total risk (as shown in the Capital Asset Pricing Model).

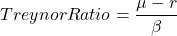
In a well-diversified portfolio Sharpe and Treynor are similar, but Treynor is more relevant for less diversified portfolios or individual stocks.

Information Ratio

The Information Ratio is a performance measure that tracks errors. The numerator represents the excess return over a benchmark, while the denominator is the standard deviation between portfolio and benchmark returns, known as the tracking error.

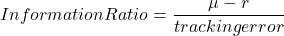
This ratio gives a measure of the value added by a manager relative to their benchmark.

Related Readings

• Modern Portfolio Theory in Finance
• Arbitrage in Quantitative Finance: All You Need To Know
• Modelling Approaches in Quantitative Finance: All You Need To Know
• Put-Call Parity: All You Need To Know