Which Numerical Methods Should be Used?
The three most common numerical methods are Monte Carlo, Finite difference, and Numerical Quadrature. (I include the binomial approach as a simplified version of finite differences.) Monte Carlo is useful for problems with complicated route dependency and high dimensionality, as well as those that cannot be expressed as differential equations. Finite difference works best in low dimensions and is compatible with choice features like early exercise, which have a different equation formulation. Numerical quadrature is used to represent option values as multiple integrals.

A Short Example of Numerical Methods
You wish to price a fixed-income contract with the BGM model. What numerical method should you use?
Since BGM is designed for simulation-based solutions, a Monte Carlo Simulation is recommended.
Consider pricing an option that may be paid in instalments, with the opportunity to cancel at any moment if payments are not worthwhile. This may be suitable for finite-difference approaches as it has a decision feature.
You wish to price a European, non-path-dependent contract on a basket of stocks. To solve this equation as a multiple integral, use the quadrature method.
Finite Difference Methods
Finite-difference methods are developed to find numerical solutions to differential equations. Using a mesh, similar to the binomial technique, we may determine the contract value at each point in stock price-time space. In quantitative finance, differential equations are typically of diffusion or parabolic form. The only significant distinction between the partial differential equations is the following:
- Number of dimensions.
- Functional form of coefficients.
- Boundary/final conditions.
- Decision features.
- Linear or non linear.
Number of Dimensions
Is the contract an option on one or more underlyings? Is there a considerable path dependence in the payoff? The answers to these questions will establish how many dimensions are in the problem. At the absolute least, we’ll have two dimensions: S or r and t. Finite-difference algorithms excel at handling fewer dimensions, such as four. Above, they become time-consuming.
Functional form of Coefficients
The principal distinction between an equity option problem and a single-factor interest rate option problem is the functional form of the drift rate and volatility. These appear as coefficients in the governing partial differential equations. The lognormal model is commonly used for stocks, although there are numerous ‘standard’ models in fixed income. Does this matter? If you’re looking for a closed-form solution, the simpler the coefficients, the more likely you’ll find one. However, this does not apply to numerical equations.
Boundary/Final Conditions
In a numerical scheme, the distinction between a call and a put is in the last condition. You instruct the finite-difference scheme how to begin. In finance, finite-difference systems begin with expiration and progress to the present. Boundary conditions inform the scheme about features such as knock-out barriers.
Decision Features
Exotic contracts have inherent decisions like as early exercise, instalment premiums, and chooser features. Dealing with these numerically is simple using finite-difference methods, making them the natural choice for such contracts. In a finite-difference programme, the difference between a European and an American option is approximately three lines of code and takes less than a minute to code.
Linear or Non-Linear
Almost all finance models are linear, allowing you to solve for a portfolio of options by solving each contract individually and adding. Some more modern models are non-linear. When using finite-difference approaches, the difference between linear and non-linear solutions is minimal. As a result, using this strategy allows you to use a wide variety of models.
Efficiency
Finite differences excel at dealing with low dimensions, and they are the preferred solution when dealing with contracts that include embedded judgements. They are ideal for nonlinear differential equations.
Using the explicit finite-difference method, it takes time to price an option and calculate the underlying(s) and time sensitivity.
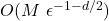
We aim for an accuracy of, where M represents the number of options in the portfolio and d represents the number of non-time dimensions. For non-path-dependent options on a single underlying, d equals 1.
Please keep in mind that each option may require a single piece of code, as indicated by M in the example above.
Monte Carlo methods
Monte Carlo methods imitate the unpredictable behaviour of financial models. So, in a sense, they get to the heart of the issue. Remember, however, that while pricing, you must simulate the risk-neutral random walk(s); the value of a contract is therefore the expected present value of all cashflows. When implementing a Monte Carlo algorithm, consider the following:
- Number of dimensions.
- Functional form of coefficients.
- Boundary/final conditions.
- Decision features.
- Linear or non linear.
Number of Dimensions
For each random factor, you must simulate a time series. It will clearly take longer to complete, but the time will be proportional to the number of components, which isn’t too bad. Monte Carlo methods excel in larger dimensions, where finite-difference methods become inefficient.
Functional form of coefficients
In reality, it makes little difference what the drift and volatility functions are, as you will not be seeking for closed-form solutions.
Boundary/final conditions
These have a similar role to finite differences. The final condition is the payment function, whereas the boundary conditions include trigger levels and other parameters.
Decision features
When a contract has embedded judgements, the Monte Carlo approach becomes difficult. This is undoubtedly the primary disadvantage of simulation methods. The Monte Carlo approach calculates option values based on current stock prices and time. To accurately price an American option, we need to understand the option value at each point in the stock price-time space. This is not normally part of the Monte Carlo solution.
Linear or non linear
Nonlinear models are also difficult for simulation systems to handle. Some models simply do not have a usable interpretation in terms of probabilities and expectancies, therefore they are unlikely to be solved using random simulation approaches.
Efficiency
If we seek an accuracy of ![]()
d underlyings, then the computation time is:
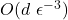
Pricing the Greeks will take longer, but it allows us to price multiple choices at once for less time expense.
Numerical Integration
Option-pricing problems can sometimes be solved using multiple integrals. The option value can be seen as a payoff expectation, which is calculated by integrating the payout function and probability density function. This is only achievable in certain situations.
For European options, the underlying stochastic differential equation must be explicitly integrable (lognormal random walk is ideal), and the reward should not be path dependent. So, if this is conceivable, pricing is simple… you have a formula. The only challenge is translating this formula into a numerical value.
This refers to numerical integration or quadrature. Watch alert for the following.
- Can you express the value of an option as an integral?
Efficiency
There are multiple numerical quadrature methods. However, the two most frequent methods rely on random number creation once more. One uses normally distributed numbers, while the other employs low-discrepancy sequences. Low-discrepancy numbers are clever because they appear random on the surface yet lack the unavoidable clustering of truly random numbers.
For pricing M choices with an accuracy of ![]()
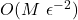
Using low-discrepancy data, the time taken will be
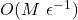
Although this procedure is quick, it is not always effective.
Summary of all the Numerical Methods discussed so far
| Subject | Finite Difference | Monte Carlo | Numerical Quadrature |
| Low Dimensions | Good | Inefficient | Good |
| High Dimensions | Slow | Excellent | Good |
| Path Dependent | Depends | Excellent | Not Good |
| Greeks | Excellent | Not Good | Excellent |
| Portfolio | Inefficient | Very Good | Very Good |
| Decisions | Excellent | Poor | Very Poor |
| Non Linear | Excellent | Poor | Very Poor |
Related Readings
- Modern Portfolio Theory in Finance
- Arbitrage in Quantitative Finance: All You Need To Know
- Modelling Approaches in Quantitative Finance: All You Need To Know
- Put-Call Parity: All You Need To Know