Modern Portfolio Theory in Finance: All You Need To Know

What is Modern Portfolio Theory?

Harry Markowitz’s Modern Portfolio Theory (MPT) analyses investment portfolios based on individual asset returns and risk, as well as their relationships. Previously, investors would focus solely on individual assets, creating portfolios of preferred stocks without considering their interrelationships. Diversification is key in MPT.

A Short Example

Should you invest all your money in a low-risk stock with a low projected return, or one with a higher expected return but greater risk? Consider dividing your money between the two. Modern Portfolio Theory helps measure and analyse risk and return.

A Deep Dive into Modern Portfolio Theory

MPT uses normal distributions with specified mean and standard deviation to depict asset returns over a given time period. One asset may have an annualised expected return of 5% and an annualised standard deviation (volatility) of 15%. Another option could have a -2% projected return and 10% volatility. Prior to Markowitz, investors would often buy in the first stock and sell the second short.
Markowitz proposed improving basic portfolios by considering the correlation of stock returns.

In the MPT world of N assets, there are 2N + N(N - 1)/2 parameters: anticipated return, standard deviation, and correlations between any two stocks (order is immaterial). Markowitz recommends comparing investments and portfolios based on projected return vs risk, measured by standard deviation. Using µA as the expected return and σB as the standard deviation, we can conclude that investment/portfolio A is comparable to B if,

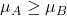 and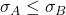 

The mathematics of risk and return is really straightforward.
Consider a portfolio, , of N assets, where represents the proportion of wealth invested in each item. The intended return is:

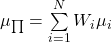
and the standard deviation of the return, the risk, is

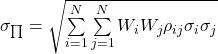
where is the correlation between the ith and jth investments, with .

Optimising Portfolio

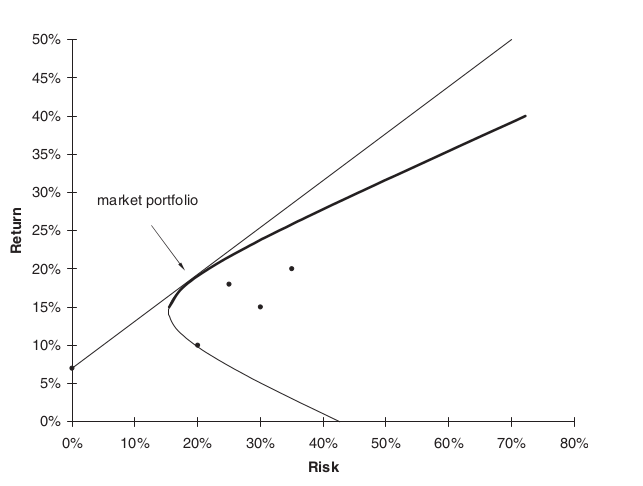
Markowitz demonstrated how to optimise a portfolio by identifying the that provide the highest projected return for a given degree of risk. The efficient frontier is the curve in the risk-return space that yields the highest predicted return for each risk level.

The notion suggests that portfolios should not fall outside the efficient frontier. Adding a risk-free investment to the asset universe results in the tangential line shown below, representing the efficient frontier. This line is called the Capital Market Line.

The Market Portfolio refers to the portfolio at its tangential point. According to the thesis, individuals should only hold risk-free investments and a market portfolio.

In 1990, Harry Markowitz, Merton Miller, and William Sharpe were awarded the Nobel Prize in Economic Science.

Related Readings

• Arbitrage in Quantitative Finance: All You Need To Know
• Modelling Approaches in Quantitative Finance: All You Need To Know
• Put-Call Parity: All You Need To Know