How Jump Diffusion Model works?
In jump diffusion model, prices are permitted to jump discontinuously in addition to the continuous Brownian motion (the diffusion) observed in Black-Scholes models. Typically, the jump’s timing is random, and a Poisson process represents this. Furthermore, the jump’s size may be at random. The values of calls and puts rise as the jump frequency increases (all other parameters staying the same). Binary and other option prices are subject to fluctuations.
A Short Example
A stock moves in a random walk that is lognormal. Each month, you take a dice roll. Should a one be rolled, the stock price will rise sharply. The amount of this jump is determined by drawing a random number out of a hat. (This is not a very good illustration because the Poisson process is not a monthly occurrence; rather, it is a continuous process.)
A Deep Dive into Jump Diffusion Model and Option Values
The Poisson process is represented by the symbol dq, which represents the jump in the random variable q from time t to time t + dt. With probability ![]()
![]()
1.
Observe how the likelihood of a jump increases with the potential jump duration, dt. The intensity of the process is represented by the scale factor ![]()
![]()
An interest rate, volatility, or equity price are examples of discontinuous financial random variables that can be modelled using this method. While studies on pure jump processes as financial models have been published, it is more common to mix jumps with traditional Brownian motion. For example, the equity model is commonly believed to represent
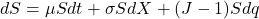
As previously mentioned, dq has an intensity of ![]()
J-1, is typically assumed to be random. Jump-diffusion models are useful for capturing the fat tails observed in return data, as well as for simulating the real-world occurrence of variable discontinuities.
A model for option prices is derived from the model for the underlying asset. Usually, this model will take the form of an integro-differential equation, where the integral term denotes the probability of the stock leaping discontinuously across a finite distance. Sadly, markets with these kinds of surges are incomplete, thus it is impossible to hedge options to remove risk. Therefore, one needs either introduce more securities to hedge or make certain assumptions about risk preferences in order to develop option-pricing equations.
History of Jump Diffusion Model
The jump diffusion model was first proposed by Robert Merton. He arrived at the following formula for the values of equity options.
![Rendered by QuickLaTeX.com \dfrac {\partial V}{\partial t} + \dfrac {1}{2}\sigma ^{2}S^{2}\dfrac{\partial ^{2}V}{\partial S^{2}}+rS \dfrac{\partial V}{\partial S} - rV + \lambda E[V(JS,t)-V(S,t)] - \lambda \dfrac{\partial V}{\partial S}SE[J-1]=0](https://thewhisperingvoid.com/wp-content/ql-cache/quicklatex.com-e37dbc9b7fbde14d4aa4490ff553fb1c_l3.png)
The expectation taken across the leap size is denoted by E[·]. This equation expresses the expected value of the discounted payout in probability terms. The true measure for the leaps is higher than the risk-neutral value for the diffusion.
In the unique situation where the logarithm of J has a normal distribution, there is an easy way to solve this equation. In the event where J‘s logarithm has a normal distribution with a standard deviation of ![]()
![Rendered by QuickLaTeX.com k = E[J-1]](https://thewhisperingvoid.com/wp-content/ql-cache/quicklatex.com-4dd1b89f4bca3ba22347081ec4a03e91_l3.png)
Consequently, the cost of a non-path-dependent European option can be expressed as
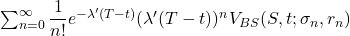
In the above equation,
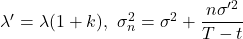
and,
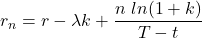
and ![]()
n leaps will have occurred before to expiry and assumes that there have been n jumps.
While other models, like stochastic volatility, struggle to capture steepness in volatility skews and smiles for short-dated options, jump diffusion model is able to do so with relative ease.
Related Readings
- Modern Portfolio Theory in Finance
- Arbitrage in Quantitative Finance: All You Need To Know
- Modelling Approaches in Quantitative Finance: All You Need To Know
- Put-Call Parity: All You Need To Know