Importance of Lognormal Distribution: All You Need to know

Why is Lognormal Distribution Important?

The lognormal distribution is commonly used to simulate the distribution of equities and commodity prices, exchange rates, and indices. The normal distribution is commonly used for modelling returns.

A Short Example

The stochastic differential equation is often used to represent equities.

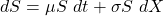
results in a lognormal distribution for S, provided and are not dependent on stock price.

A Deep Dive into Lognormal Distribution

Lognormal distribution occurs when a quantity’s logarithm follows a normal distribution, as defined.
The probability density function is:

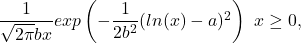
The values a and b > 0 indicate location and scale. The distribution is tilted to the right, reaching infinity and confined below by zero. (The left limit can be adjusted to add a parameter, or reflected vertically to extend to minus infinity.)

Using the preceding stochastic differential equation, the probability density function for S based on time and parameters is

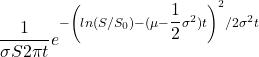
where is the value of S at time t = 0.

Equity prices typically follow a random walk around an exponentially increasing average. Take the logarithm of the stock price and expect it to be normal around a mean. This is the non-mathematical explanation behind the lognormal distribution.

Lognormality can be supported mathematically by using the Central Limit Theorem. Using to represent the random return on a stock price from day i-1 to day i, we get

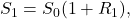
The stock price increases with the return from day zero (beginning value) to day 1. Following the second day, we have

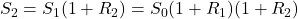
After n days we have,

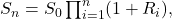
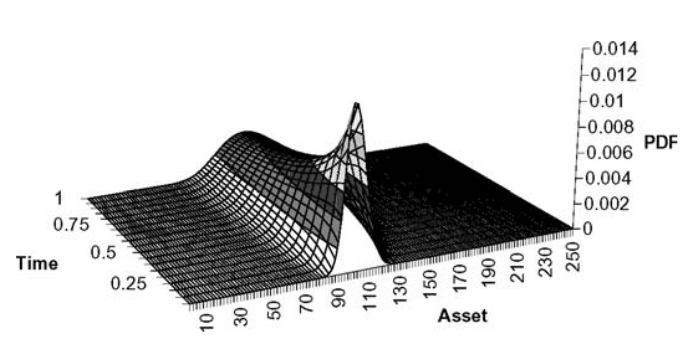
The stock price is calculated by multiplying the beginning value by n factors, where each factor represents one plus the random returns. Taking logarithms of this, we obtain

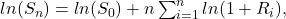
the logarithm of a product being the sum of the logarithms.

Conclusion

Now consider the Central Limit Theorem. If each is unpredictable, so is . The expression for is simply a big accumulation of random numbers. If the are independent and identically distributed, and the mean and standard deviation of are finite, we can use the CLT to deduce that is normally distributed. Thus, is regularly distributed. The mean of will rise linearly with the number of ‘days’ (or any defined time period), whereas the standard deviation will expand proportionally to the square root of n, similar to how time grows.

Related Readings

• Modern Portfolio Theory in Finance
• Arbitrage in Quantitative Finance: All You Need To Know
• Modelling Approaches in Quantitative Finance: All You Need To Know
• Put-Call Parity: All You Need To Know