What is Bootstrapping?
Bootstrapping involves creating a forward interest-rate curve that aligns with the market pricing of common fixed-income products like bonds and swaps. The curve can be used to appraise non-tradable instruments like bonds.

A Short Example
You’re familiar with bond market values for maturities ranging from one to five years. You are asked to assess the value of a four-year bond. How can you use traded prices to ensure a steady four-year bond price?
A Deep Dive into Bootstrapping
Assume interest rates change deterministically, with no unpredictability. Interest rates may increase in the future, even if they are now low. The spot interest rate refers to the amount of interest earned in a given moment. In a deterministic interest-rate environment, the spot rate can be expressed as a function of time, r(t). Understanding this function allows you to use the discount factor to value fixed-coupon bonds of any maturity.
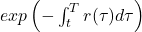
to present value a payment at time T to today, t.
Unfortunately, you are not told what the r function is. Market pricing of fixed-income instruments provide insight into the limits on the r function.
For instance, if a $100 zero-coupon bond matures in a year and is worth $95 today, we can conclude that
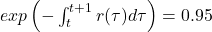
Assuming an identical two-year zero-coupon bond is worth $92, then follows that
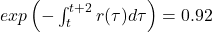
This information is insufficient to calculate the entire r(t) function, but it is comparable to what we encounter in practice. The r(t) function is constrained by various instruments, including bonds with and without coupons, as well as liquid swaps with various maturities.
Bootstrapping involves backing out a deterministic spot rate function, r(t), commonly known as the forward rate curve, which is consistent with all liquid instruments.
Interpolation Techniques for Forward Curves
Bootstrapping typically involves simple ‘linear’ instruments. This refers to bonds and swaps, which can be combined to create a bond portfolio. Contracts with caps and floors require a stochastic model for interest rates due to their optionality. Assuming a deterministic scenario for these instruments is not financially viable, similar to assuming a deterministic stock price path for equity options.
Because the forward rate curve is not uniquely determined by the finite set of limitations that we face in actuality, we must impose certain limits on the function r(t).
Finding a forward curve with these features involves interpolating ‘between the points,’ where the ‘points’ represent the constraints on the integrals of the r function. Several interpolation techniques have been proposed, including:
- linear in discount factors, spot rates, logarithm of rates
- piecewise linear continuous forwards
- cubic splines
- Bessel cubic spline
- monotone-preserving cubic spline
- quartic splines
The approach should provide a forward rate function that is not very sensitive to input data, bond prices, and swap rates. It should also be rapid to compute and not excessively local, meaning that changes to one input should only affect surrounding functions.
It’s important to note that there is no “correct” way to connect the dots.
Deposit rates are typically used for the short term, bonds and FRAs for the medium term, and swaps for the long term due to their relative liquidity.
The bootstrapped forward curve assumes deterministic rates, making it unsuitable for pricing convex instruments that require a randomness model (Jensen’s Inequality explains why).
Related Readings
- Modern Portfolio Theory in Finance
- Arbitrage in Quantitative Finance: All You Need To Know
- Modelling Approaches in Quantitative Finance: All You Need To Know
- Put-Call Parity: All You Need To Know