Utility Function in Finance: All You Need to Know

What is Utility Function?

A utility function evaluates the value, happiness, or satisfaction of commodities, services, events, outcomes, and wealth levels. It can rate results, aggregate ‘pleasure’ among individuals, and value chance-based games.

A Short Example

You plan to sell a valuable work of art at auction. The auctioneer has assessed the likelihood of achieving specific sums, but you have no idea how much you will earn. Someone offers you a guaranteed amount if you withdraw the painting from the auction. Should you accept the offer or take your chances? Utility theory can assist you make this decision.

A Deep Dive into Utility Function

Although not commonly employed in finance, this concept is widely discussed in literature, particularly in economics. The utility function ranks incomparable items and explains human behaviour. Rational individuals aim to maximise their utility.

Cardinal utility refers to the use of meaningful numerical values to convey utility. The utility of one thing can be three times that of another, and can be compared across individuals. Ordinal utility refers to the ordering of preferences rather than their numerical value.

Utility functions, denoted as U(W) where W represents ‘wealth’ are expected to exhibit sensible features. The following represents difference with respect to W.

• Investors’ risk tolerance may differ, resulting in a unique function U(W).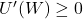
• indicates that more is desired over less. Satisfaction is impossible when there is a rigid inequality, as the investor would constantly want more than what they have. This slope represents the marginal increase in utility with wealth changes.
• Typically, the utility function is severely concave, with . As money accumulates, increasing marginal ‘happiness’ becomes increasingly challenging. An investor with a concave utility function is considered risk averse. This property is known as the law of diminishing returns.

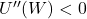
The final item provides definitions for measuring risk aversion. The absolute risk aversion function is described as

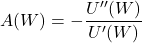
The relative risk aversion function is defined as

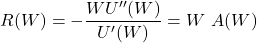
Usage of Utility Function

Utility functions are commonly used for analysing random events. Assume a monetary value correlates with the number of spots on a rolled dice. To determine the expected wins, take the average of all six amounts. What if the quantities were $1, $2, $3, $4, $5, or $6,000,000? Is the average of $1,000,002.5 meaningful? Are you willing to pay $1,000,000 to enter this bet? You anticipate to make a profit. To accurately value this game, consider the usefulness of each of the six outcomes and average them. This leads to the concept of confidence equivalent riches.

When wealth is random and all outcomes have a probability, it’s possible to determine how much certain wealth equals the expected utility of unknown outcomes. Simply solve.

The amount of wealth , The solution to this equation is known as certainty equivalent wealth. There is no significant difference between the average utility of random events and the promised amount . For example, in the dice-rolling game, suppose our utility function is

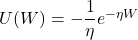 with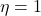 

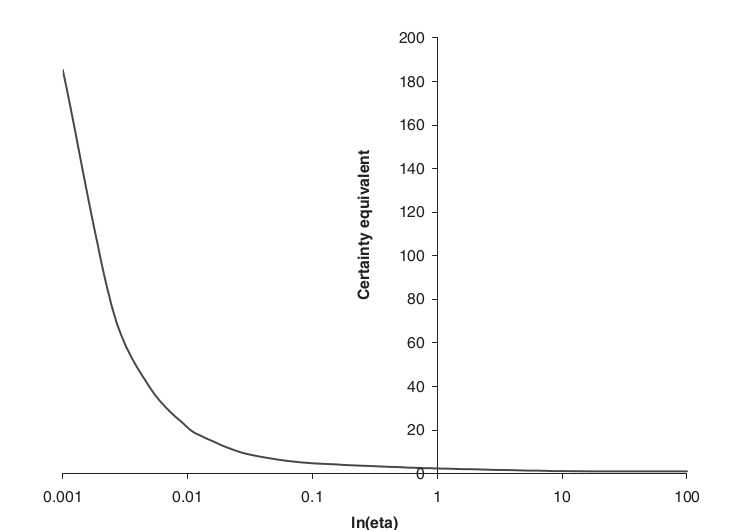
We calculate that the certainty equivalent is $2.34. We would pay this amount or less to play the game. The graphic above shows the certainty equivalent for this example as a function of the risk-aversion parameter, $eta $. Observe how this reduces with increased risk aversion.

Related Readings

• Modern Portfolio Theory in Finance
• Arbitrage in Quantitative Finance: All You Need To Know
• Modelling Approaches in Quantitative Finance: All You Need To Know
• Put-Call Parity: All You Need To Know