What is Capital Asset Pricing Model?
The Capital Asset Pricing Model (CAPM) compares the returns on individual assets or portfolios to the market as a whole. It introduces the ideas of particular and systematic risk. Specific risk is specific to an asset, while systematic risk is related with the market. CAPM compensates investors for systematic risk, not specific risk. Diversification of investments can reduce specific risk.

A Short Example
A stock’s projected return is 15%, with a volatility of 20%. But how much of that risk and return is due to the market as a whole? Because the less that can be attributed to market activity, the better a stock is for diversification.
A Deep dive into Capital Asset Pricing Model
CAPM simplified Markowitz’s Modern Portfolio Theory (MPT), introducing the concept of specific and systematic risk. Whereas MPT has an arbitrary correlation between all investments, CAPM, in its basic form, simply connects investments through the market as a whole.
In contrast to Black-Scholes, which is a no-arbitrage model, CAPM is an equilibrium model.
CAPM’s mathematics are fairly basic. We compare the random return on the ith investment, Ri, to the random return on the market as a whole (or a representative index), RM, by
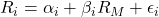
The i is a random variable with zero mean and standard deviation ![]()
RM and the other j. Each asset has three parameters (![]()
i). The random portion i is exclusive to the ith asset. Note how all of the assets are tied to the index but otherwise uncorrelated.
Understanding Alpha and Beta in Investment Strategies
Let us denote the expected return on the index by ![]()
![]()
ith asset is now
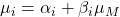
and the standard deviation
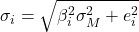
If we have a portfolio of such assets then the return is given by
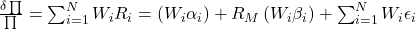
From this it follows that
![Rendered by QuickLaTeX.com \mu _{\prod} = \left ( \sum _{i = 1}^{N}W_i\alpha _i + E[R_M] + \left ( \sum _{i = 1}^{N}W_i \beta _i \right )\right )](https://thewhisperingvoid.com/wp-content/ql-cache/quicklatex.com-536144a1976c97c08e31e5fdc8f3f145_l3.png)
Writing
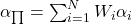 and
and 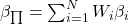
we have,
![Rendered by QuickLaTeX.com \mu _{\prod} = \alpha _{\prod} + \beta _{\prod}E[R_M] = \alpha _{\prod} + \beta _{\prod}\mu _M](https://thewhisperingvoid.com/wp-content/ql-cache/quicklatex.com-b6cd744d24fd892baebb25614749c59b_l3.png)
Similarly the risk in ![]()
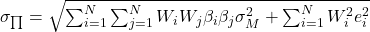
If the weights are about equal N-1 , the final terms in the square root will also be ![]()
N approaches ![]()
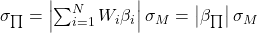
Observe that the contribution of uncorrelated assets to the portfolio diminishes as the number of assets in the portfolio grows; this is the risk associated with diversifiable risk. The remaining risk, connected with the index, is the undiversifiable systematic risk.
Hedge Fund Strategies
CAPM can be implemented using many indexes. Each index represents an important financial or economic variable.
In the hedge-fund industry, the terms alpha and beta are also often used. Trading strategy performance reports typically include alpha and beta values. A successful approach will have a strong positive alpha and a beta close to 0. A low beta indicates unconnected performance to the market, whereas a high alpha indicates positive returns regardless of market direction. A strategy with a low beta might add value to a portfolio by providing diversification.
Sharpe received the 1990 Nobel Prize in Economics alongside Harry Markowitz and Merton Miller.
Related Readings
- Modern Portfolio Theory in Finance
- Arbitrage in Quantitative Finance: All You Need To Know
- Modelling Approaches in Quantitative Finance: All You Need To Know
- Put-Call Parity: All You Need To Know